常用数据结构。

栈和队列(Stack & Queue)

性质

• 栈是一种后进先出(LIFO)的线性表，插入和删除数据元素的操作只能在线性表的一端进行。
• 队列是一种先进先出(FIFO)的线性表。传统的队列中，插入只能在表的一端进行(只进不出)，而删除只能在表的另一端进行(只出不进)。允许插入的一端称为队头，允许删除的一端称为队尾。不过，目前主流语言都支持双头队列，标准比起传统队列相对宽松，允许两头都进，两头都出。

时间复杂度

栈

• 插入: O(1)
• 删除: O(1)
• 查找: O(n)
• 最值: O(1)

队列

• 插入: O(1)
• 删除: O(1)
• 查找: O(n)
• 最值: O(1)

一般二叉树(Binary Tree)

性质

二叉树是有限个节点的集合，这个集合或者是空集，或者是由一个根节点和两株互不相交的二叉树组成，其中一株叫根的做左子树，另一棵叫做根的右子树。

• 在二叉树中第i层的节点数最多为2（i ≥ 1）
• 高度为k的二叉树其节点总数最多为2 - 1（k ≥ 1）

完全二叉树

除最后一层外，每一层上的节点数均达到最大值；在最后一层上只缺少右边的若干节点；具有n个节点的完全二叉树的深度为log(n + 1)。

二叉搜索树(Binary Search Tree)

性质

一种特殊的二叉树，对于二叉搜索树上的每个节点，若它的左子树不空，则左子树上所有节点的值均小于这个节点的值； 若它的右子树不空，则右子树上所有节点的值均大于这个节点的值。

时间复杂度

• 插入: O(logn)
• 删除: O(logn)
• 查找: O(logn)

红黑树(Red Black Tree)

性质

一种特殊的二叉平衡树，有5个特点:

• 每个节点可能是红色或黑色
• 根节点是黑色
• 有虚拟的黑色NIL叶子
• 如果某个节点是红色的，它的两个子节点都是黑色的
• 从一个节点到任意一个虚拟的后代NIL叶子节点的路径上，经过的黑色节点数相等

时间复杂度

• 插入: O(logn)
• 删除: O(logn)
• 查找: O(logn)

应用

Java中的HashMap, TreeMap, TreeSet等

堆(Heap)

性质

一种特殊的完全二叉树。有两种堆：

• 最小堆，非叶子节点的值不大于左子或右子的值（根节点的值最小）
• 最大堆，非叶子节点的值不小于左子或右子的值（根节点的值最大）

堆可以应用于priority queue和堆排序

建堆时间 & 空间复杂度

建堆的两种方法：

• forward method，逐个地获取到数据节点，插入到堆中调整位置来构建堆。需要 n * O(logn) = O(nlogn)的时间复杂度。这种方法适合流式传输数据 / 无法提前获取到所有数据的情况
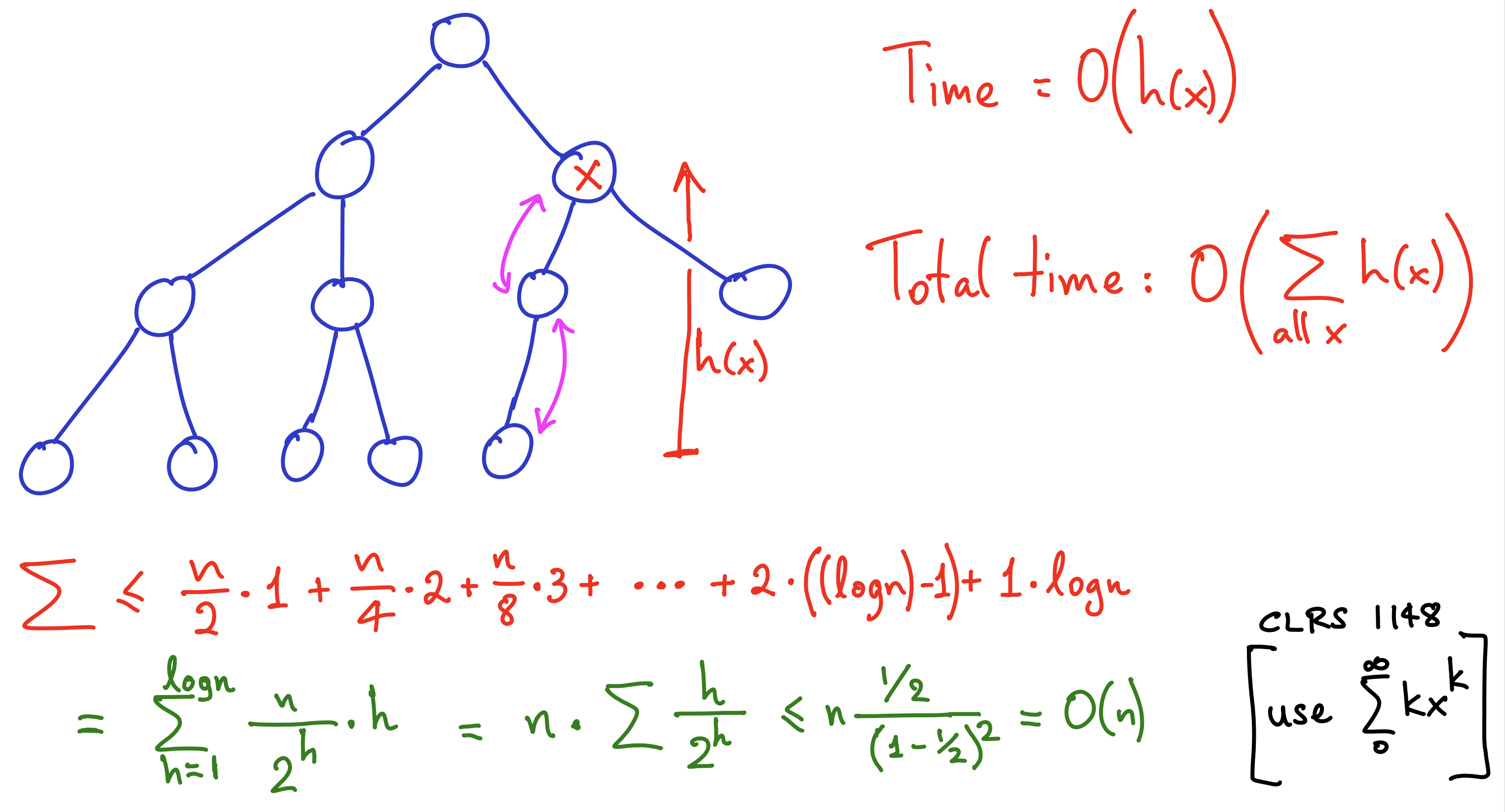
• reverse method，在已知所有数据的情况下，从底向上，每一层从右到左，尝试进行父节点和子节点的交换（如果有必要的话）。所有节点的调整时间总和是O(n)。

复杂度分析： 空间复杂度是O(1)，因为是原地操作；对堆进行调整，需要从根节点往下循环查找，需要O(logn)的时间。

节点删除后堆的维护

先将堆的最后一个元素（最底层，最靠右）移动到根节点，之后从根节点自上而下递归调整，看每个父节点跟子节点是否需要交换。

数组 vs. 链表

主要区别

数组是线性表，所有元素存储在连续的内存空间中。数组可能是定长的（需要提前申请定量内存），但动态数组(Vector, ArrayList, …)一般是resizable的，达到capacity阈值后容量不断倍增。数组适合高随机访问，少插入/删除的场景。

链表的元素存储在不连续的内存空间中，每个数据保存了下一个地址的内存数据。不需要定义内存大小。链表适合高插入/删除，少随机访问的场景。

时间复杂度

数组：

• 插入: 随机位置是O(n)，末尾是O(1)
• 删除: 随机位置是O(n)，末尾是O(1)
• 读取: O(1)

链表:

• 插入: O(1)
• 删除: O(1)
• 读取: O(n)

哈希表(Hash Table)

性质

根据关键码值 (Key-Value) 而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。

设计注意事项

• 构造一个合理的哈希函数
  • 对于不同的输入应该产生不同的结果，输出值应该尽量均匀
  • 输入的微小变化会导致输出的较大变化
• 解决不同输入，相同输出的冲突问题
  • 链地址法，为每个哈希值建立一个单链表，当发生冲突时，将记录插入到链表中。
  • 开放定址法，所有的元素都放在散列表中，用探针不断确定下一个位置来检查所有数据项。要求是表要足够大，一般是所有数据个数的整数倍。

时间复杂度

平均而言，哈希表的插入/删除/查找操作时间复杂度是O(1)，但是在最差情况下（链地址法，多次碰撞冲突）会退化到O(n)。

字典(Map)

性质

一种存放键值对的容器。有以下几种类型：

• 无序哈希表(Hashmap in Java, unordered_map in C++)

  本质上是哈希表，将key做hash算法，然后将hash值映射到内存地址，直接取得key所对应的数据。所谓的内存地址即数组的下标索引。不能保证插入的数据是有序的。

• 带双向链表的哈希表(LinkedHashMap in Java)

  额外维护了一个双向链表用于保持迭代顺序。以Java的LinkedHashMap为例，其默认实现是按插入顺序排序的。

• 有序哈希表 (TreeMap in Java, map in C++)

  本质上是红黑树，插入数据时按照key的大小自动进行排序。TreeMap具备良好的统计性能（例如找最大/最小的key，或者有几个key比3大等等），可以在O(logn)时间内完成。

时间复杂度

无序哈希表:

• 插入: O(1)
• 删除: O(1)
• 查找: O(1)，但是在最差情况下（链地址法，多次碰撞冲突）会退化到O(n)

带双向链表的哈希表:

• 插入: O(1)
• 删除: O(1)
• 查找: O(1)，但是在最差情况下（链地址法，多次碰撞冲突）会退化到O(n)

有序哈希表:

• 插入: O(logn)
• 删除: O(logn)
• 查找: O(logn)

集合(Set)

一个不允许出现重复元素的容器。以Java语言为例：

• HashSet：基于HashMap实现，插入元素时，所有元素的value都指向一个Object对象，因此HashSet用不到HashMap的value，所以不会为其分配一个内存空间
• TreeSet：基于TreeMap实现，操作数据的方法与HashSet调用HashMap类似
• LinkedHashSet：基于LinkedHashMap实现，操作数据的方法与HashSet调用HashMap类似

因为Set全部基于Map实现，因此时间复杂度与Map保持一致。

图(Graph)

性质

一种复杂的非线性结构，由节点和边组成。节点之间的关系是任意的，图中任意两个数据元素之间都有可能相关。根据边是否具有指向性，可以将图分为有向图和无向图。

图一般有以下两种表现形式：

• 邻接矩阵

  节点之间如果有边相连，用1表示，反之是0。大小: V

• 邻接表

  每个节点维护一个链表，存储这个节点分别和其他哪些节点通过边连接。大小: V + 2E (无向图)，V + E (有向图)

复杂度

邻接矩阵的空间复杂度: O(V)；邻接表的空间复杂度: O(V + E)

• 查找某个节点是否为相邻节点

  邻接矩阵: O(1) 邻接表: O(V)

• 列举某个节点的所有相邻节点

  邻接矩阵: O(V) 邻接表: O(V)

跳表(Skiplist)

性质

跳表是受这种多层链表的想法的启发而设计出来的特殊数据结构。

对一个有序链表，通常来说如果要查找某个数据，需要从头开始逐个比较，直到找到包含数据的节点，或者第一个比给定数据大的节点为止（没找到）；假如每相邻两个节点增加一个指针，让指针指向下下个节点，这样所有新增加的指针连成了一个新的链表，但它包含的节点个数只有原来的一半。当我们想查找数据的时候，可以先沿着这个新链表进行查找，当碰到比待查数据大的节点时，再回到原来的链表中进行查找。利用同样的方式，我们可以在上层新产生的链表上，不断为每相邻的两个节点增加一个指针；程序总是从高层先开始访问，然后随着元素值范围的缩小，慢慢降低层次……按照上面生成链表的方式，上面每一层链表的节点个数，是下面一层的节点个数的一半，这样查找过程就非常类似于一个二分查找。

但是，上述方法在插入数据的时候有很大的问题。新插入一个节点之后，会打乱上下相邻两层链表上节点个数严格的2:1的对应关系。要维持这种对应关系，必须把新插入的节点后面的所有节点（也包括新插入的节点）重新进行调整，这会让时间复杂度重新蜕化成O(n)。删除数据也有同样的问题。跳表为了避免这一问题，它不要求上下相邻两层链表之间的节点个数有严格的对应关系，而是为每个节点随机出一个层数(level)，新插入一个节点不会影响其它节点的层数。因此，插入操作只需要修改插入节点前后的指针，而不需要对很多节点都进行调整。比如，一个节点随机出的层数是3，那么就把它链入到第1层到第3层这三层链表中。以下是一个例子：

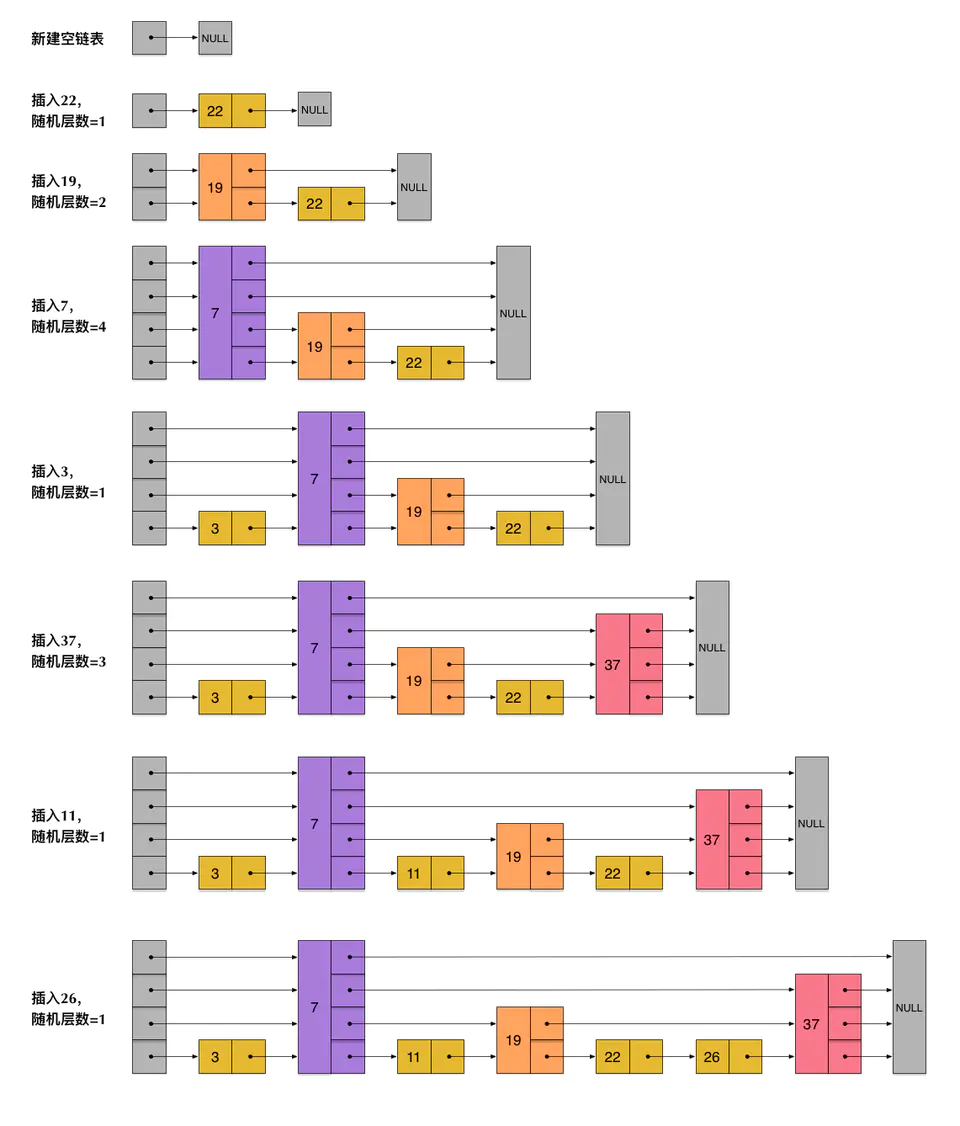
执行插入操作时计算随机数的过程十分关键，它并不是一个普通的服从均匀分布的随机数，需要满足一些条件：

• 每个节点肯定都有第1层指针（每个节点都在第1层链表里）。
• 如果一个节点有第i层(i >= 1)指针（即节点已经在第1层到第i层链表中），那么它有第(i+1)层指针的概率为p(Redis中取值为0.25)。
• 节点最大的层数不允许超过一个最大值，记为MaxLevel(Redis中取值为32)。

时间复杂度

• 插入：O(logn)
• 删除：O(logn)
• 查找：O(logn)